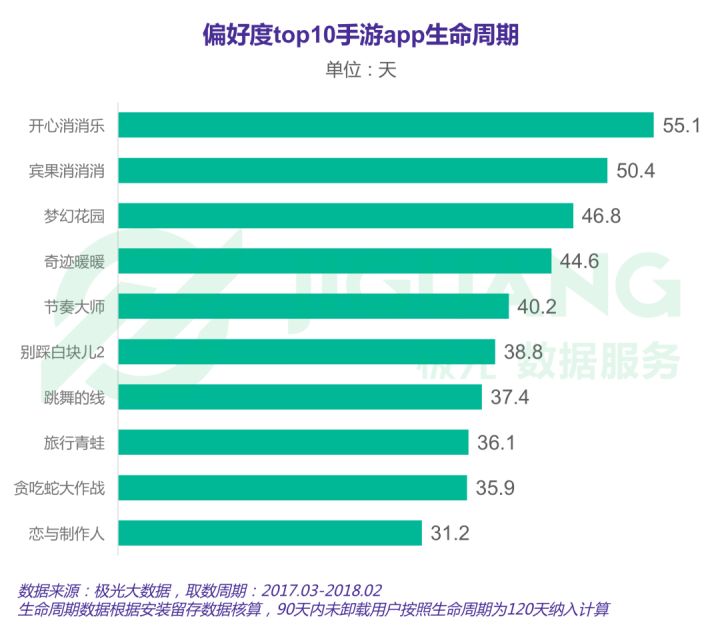
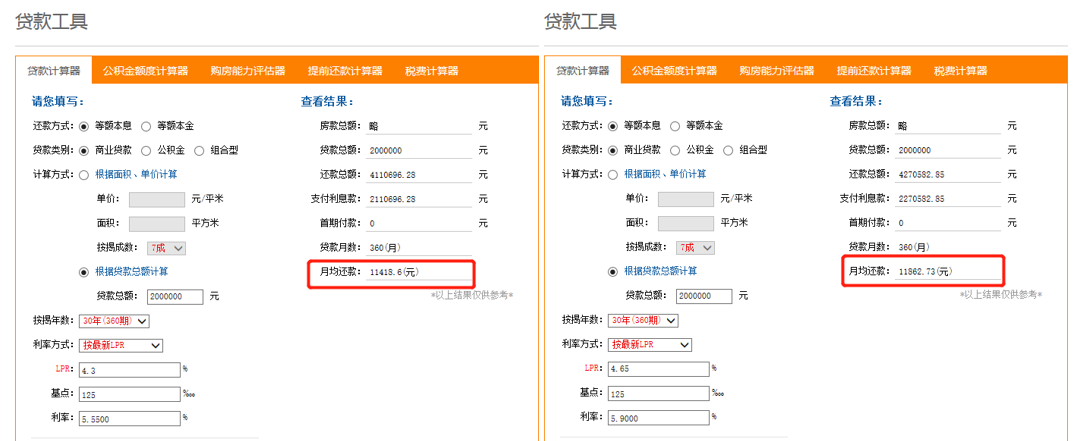
拉普拉斯变换，解析数学工具的魅力-拉普拉斯变换

拉普拉斯变换作为数学领域的一种强大工具，广泛应用于工程、物理等多个领域，通过对信号或函数进行拉普拉斯变换，我们能更深入地理解其性质和特点，进而解决实际问题，本文将详细介绍拉普拉斯变换的基本概念、性质、应用及其在实际问题中的意义。

拉普拉斯变换的基本概念

拉普拉斯变换是一种积分变换，它将实数域上的函数转换为复数域上的函数，对于实数域上的函数f(t)，其拉普拉斯变换定义为：

F(s) = ∫₀⁺∞ f(t)e⁻³³ dt

s为复数，t为时间变量，拉普拉斯变换的主要目的是将时间域中的函数转换为频率域中的函数，从而方便分析和处理。

拉普拉斯变换的性质

拉普拉斯变换具有许多重要的性质，这些性质为信号和系统的分析提供了有力的工具，以下是几个重要的拉普拉斯变换性质：

1、线性性质：对于两个函数的和或差的拉普拉斯变换等于各自拉普拉斯变换的和或差。

2、时移性质：时移函数的拉普拉斯变换可以通过原函数的拉普拉斯变换与复指数函数的乘积来表示。

3、频移性质：频移函数的拉普拉斯变换可以通过原函数的拉普拉斯变换与复正弦函数的乘积来表示。

4、微分性质：原函数导数的拉普拉斯变换等于其拉普拉斯变换乘以负s。

5、积分性质：原函数积分的拉普拉斯变换等于其拉普拉斯变换的积分形式。

拉普拉斯变换的应用

拉普拉斯变换在各个领域有着广泛的应用，尤其在电气工程、机械工程、通信工程和控制系统等领域，以下是几个典型的应用实例：

1、电气工程：在电力系统中，拉普拉斯变换可用于分析电路的频率响应，确定系统的稳定性和性能，它还可用于分析电力电子电路中的开关电源和滤波器。

2、机械工程：在机械工程中，拉普拉斯变换可用于分析机械系统的动态响应，如振动和冲击，通过拉普拉斯变换，可以方便地求解系统的传递函数和频率响应。

3、通信工程：在通信系统中，拉普拉斯变换可用于信号处理和分析，调制和解调过程可以通过拉普拉斯变换来实现，提高信号的传输质量。

4、控制系统：在控制系统中，拉普拉斯变换是分析和设计控制系统的重要工具，通过求解系统的传递函数，可以判断系统的稳定性、确定系统的性能指标，并进行系统优化。

拉普拉斯变换的实际意义

拉普拉斯变换作为一种强大的数学工具，具有深远的实际意义，它将时间域问题转换为频率域问题，简化了复杂系统的分析过程，它为系统设计和优化提供了有力的支持，使工程师和科学家能够更准确地预测和控制系统行为，拉普拉斯变换还可用于解决各种实际问题，如信号处理、电路分析、机械振动等，为各个领域的发展做出了巨大贡献。

本文详细介绍了拉普拉斯变换的基本概念、性质、应用及其在实际问题中的意义，作为一种强大的数学工具，拉普拉斯变换在各个领域发挥着重要作用，通过深入了解拉普拉斯变换的原理和应用，我们可以更好地理解和分析复杂系统，为实际问题的解决提供有力支持。